Menurut Prasetyo (2013), fisika merupakan cabang ilmu
pengetahuan alam atau sains yang pada dasarnya memiliki hakikat sama dengan
sains itu sendiri. Umumnya ilmu fisika adalah ilmu yang berkaitan erat dengan
ilmu matematika. dimana teori fisika banyak dinyatakan dalam notasi matematis.
Perbedaan antara fisika dan matematika adalah fisika berkaitan dengan dunia
material, sedangkan matematika berkaitan dengan pola-pola abstrak yang tak
selalu berhubungan dengan dunia material (Agnes, 2019). Ada wilayah luas
penelitIan yang beririsan antara fisika dan matematika, yakni fisika matematis,
yang mengembangkan struktur matematis bagi teori-teori fisika (Ishaq, 2007).
Sebagian orang berpendapat bahwa fisika merupakan hal
yang sulit. Hal tersebut dikarenakan fisika sangat erat hubungannya dengan
perhitungan. Sama hal nya dengan anggapan mengenai matematika (Hugh dan Roger,
2002).
Fisika dapat dipelajari melalui 3 metode secara garis
besar, yaitu menggunakan memakai pemahaman konsep atau menggunakan teori fisika
yang bisa melahirkan teori fisika. Selanjutnya yaitu melalui
eksperimen/pengamatan yang bisa menciptakan suatu fisika eksperimental.
Terakhir, melalui simulasi tanda-tanda kenyataan alam disekitar kita yang sangat didukung teknologi dan paduan berfikir melalui
algoritma berupa angka-angka (Said, 2015).
Pada umumnya teori komputasi merupakan suatu ilmu yang menekankan dalam penyusunan contoh matematika disertai penyelesaian numerik yang bisa memecahkan duduk perkara pada dunia sains. Fokus makalah ini berisikan mengenai pencocokan kurva yang merupakan teknik yang penting dan sangat diperlukan untuk menanganidata hasil pengukuran suatu variabel, sehingga diperoleh gambaran jelas mengenai sifat-sifat atau perilaku variabel yang kita ukur. Pembahasan kali ini meliputi metode pencocokan kurva interpolasi dan ekstrapolasi, menentukan persamaan kurva, disertai contoh soal.
Pencocokan Kurva
Pencocokan Kurva (Curve Fitting) adalah salah satu
metode dalam mengestimasi kurva/garis yang mewakili serangkaian titik data (Al
Rusman, dkk, 2016). Terdapat dua alasan mengapa pencocokan kurva dari data hsil
pengukuran sangat penting. Pertama, hal tersebut karena dengan cara fitting
akan dapat memberikan gambaran sistematis tentang hubungan dua variable yang
akan diukur. Dan dari persamaan kurva yang dipeoleh digunakan untuk
memprediksikan harga variabel tak bebas di suatu titik dengan cara
menginterpolasi diantara harga-harga terukur (Rendi, 2020).
Terdapat dua metode dalam curve fitting
(pencocokan kurva) yaitu regresi dan interpolasi. Perbedaan antara keduanya
terletak pada error. Regresi adalah metode atau cara menentukan persamaan yang
melewati kumpulan titik, namun tidak semua titik dapat dengan tepat dilewati
fungsi/persamaan regresi. Sedangkan interpolasi secara sederhana diartikan
sebagai metode yang digunakan untuk menentukan fungsi yang sesuai dari titik-titik
yang berikan.
Interpolasi/ekstrapolasi bertujuan untuk membangun suatu kurva yang melalui semua titik data. Interpolasi kurva yang dibangun dipakai untuk menaksir f(x) nilai dengan x berada di dalam interval titik-titik data yang diberikan. Sedangkan ekstrapolasi merupakan kurva yang dibangun dipakai untuk menaksir nilai f(x) dengan x berada di luar interval titik-titik data yang diberikan.
Metode Pencocokan Kurva
Metode yang paling sederhana untuk mencocokkan data kepada suatu kurva
tertentu adalah dengan mengeplot titik-titik data tersebut dan menarik garis
yang bersesuaian dengan data tersebut. Kalau hal ini yang dilakukan, maka
masalah yang timbul kemudian adalah cara menginterpretasikan data hasil
pengukuran tersebut Dalam hal ini jelas akan bergantung kepada subyektivitas
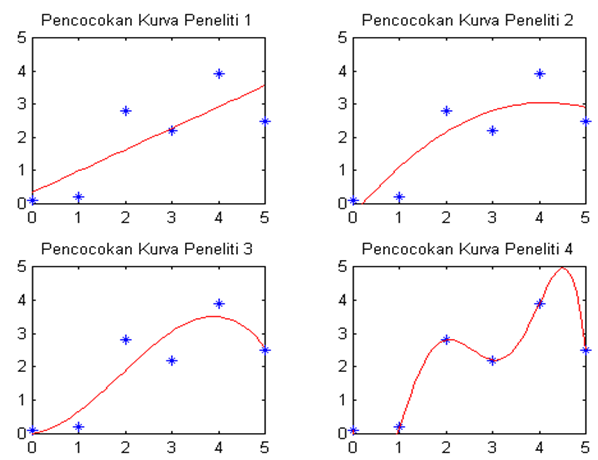
dari peneliti itu sendiri. Sebagai contoh, pada gambar 1 ditampilkan empat
hasil pencocokan data kepada kurva yang dilakukan oleh empat peneliti.
1. Regresi Linier
Regresi linier adalah sebuah metode pencarian persamaan linier berdasarkan pada seperangkat titik data hasil pengukuran. Untuk lebih jelasnya, kita akan mengambil sebuah contoh data pengukuran suhu dalam sepuluh menit seperti terlihat pada tabel 1. Dengan data yang kita miliki tersebut, kita dapat menarik garis semau kita yang sama-sama dekat dengan titik data, meskipun tidak ada satupun garis melewati tepat pada titik-titik data tersebut (lihat gambar 1. Pertanyaan selanjutnya adalah, bagaimanakah caranya untuk memperoleh persamaan garis yang cocok dengan data pengukuran itu sehingga diperoleh simpangan minimal. Untuk tujuan ini, dimisalkan fungsi pendekatan linier ini dinyatakan oleh
dimana a dan b merupakan konstanta-konstanta sembarang.
 |
| Gambar 2. Plot data pengukuran dari tabel 1 |
Penyimpangan setiap titik data dengan fungsi dinyatakan
oleh
dengan M merupakan jumlah total titik-titik data. Simpangan harga antara besaran yang teramati (observed value) yang dinyatakan oleh yi dengan harga prediksi (predicted value) yang dinyatakan oleh y(xi) juga. sering disebut residu. Dalam contoh tersebut kita memiliki sebelas titik data, dengan a dan b merupakan konstanta-konstanta yang akan ditentukan kemudian. Selanjutnya, kita dapat menyatakan total kuadrat simpangan data (residu) diberi- kan oleh
Oleh karena a dan b merupakan parameter-parameter sembarang, maka
untuk menentukan harga dari dua parameter tersebut harus dilakukan dengan cara
meminimisasi D. Minimisasi terhadap
total kuadrat simpangan dinyatakan dengan menurunkan satu kali D terhadap
parameter a dan b, atau jika dituliskan secara matematis bentuknya adalah
Persamaan di atas dapat dinyatakan kembali sebagai
Sehingga kita dapat mendefinisikan bentuk-bentuk
jumlahan (sum) sebagai berikut
Dalam persamaan
tersebut indeks i bergerak dari 1 sampai
M.
Atau jika
disajikan dalam bentuk matriks, maka persamaan linier 7) dapat dituliskan
kembali menjadi
Penyelesaian dua
persamaan linier simultan dengan dua variabel tak diketahui dapat dinyatakan
sebagai
dimana
2. Pencocokan Data
dengan Fungsi Eksponensial
Metode regresi
linier dapat pula digunakan untuk mencocokkan data terhadap fungsi-fungsi
eksponensial dalam beberapa kasus. Kita ingat kembali, secara umum fungsi
eksponensial dapat dinyatakan sebagai
Dalam hal ini,
fungsi eksponensial memerikan banyak fenomena yang berbeda-beda di dalam ilmu
teknik. Parameter a dan b dapat kita tentukan dengan sedikit manipulasi
matematis dasar. Misalnya sekarang kita ambil logaritma alamiah untuk kedua
ruas persamaan 10), maka kita peroleh ungkapan
Dengan menggunakan definisi
maka persamaan 8) menjadi
u = bx + c ... 13)
yang merupakan persamaan garis lurus (tetapi perlu diingat bahwa bentuk ini tidak sama dengan persamaan garis lurus yang kita kenalkan sebelumya). Jadi kita dapat mencocokkan seperangkat data dengan suatu fungsi eksponensial dengan cara seperti yang kita lakukan pada garis lurus. Dengan mensubstitusi u atau ln (y) untuk variabel tak bebas, parameter b untuk lereng (slope) dan c untuk perpotongan pada sumbu u, maka kita memperoleh satu garis lurus, yaitu
Jika ditampilkan dalam bentuk matriks, maka persamaan 14) menjadi
Dari ungkapan matriks 15), maka koefisien b dan c dapat ditentukan
masing-masing adalah
Selanjutnya, koefisien a dapat
diperoleh kembali dengan mengambil antilogaritma dari parameter c yang sudah kita ketahui harganya,
yaitu
3. Pencocokan Data
Menggunakan Fungsi Berpangkat
Fungsi
berpangkat merupakan fungsi matematis yang memiliki bentuk umum
dengan a dan b merupakan konstanta-konstanta persamaan linier yang akan
ditentukan melalui teknik regresi linier. Untuk menerapkan metode kuadrat
terkecil pada persamaan 18) tersebut, maka kita harus mengambil logaritma
alamiahnya pada kedua ruas persamaan sehingga diperoleh ungkapan
Dengan
menggunakan definisi
maka persamaan
(2-19) dapat kita tuliskan kembali menjadi
v = bu + c ... 21)
yang merupakan
persamaan untuk garis lurus. Untuk menerapkan metode kuadrat terkecil pada
masalah ini, maka dapat dilakukan langkah-langkah analogi pada ungkapan 4)
sampai dengan 8) sehingga diperoleh ungkapan
Sehingga
harga-harga untuk konstanta a dan b dapat ditentukan melalui hubungan
Setelah ditemukan
harga untuk parameter b dan c, maka harga a dapat ditemukan kembali melalui hubungan
4 Regresi
Polinomial
Pada pembahasan terdahulu kita telah membicarakan tentang
regresi linier yang bekerja pada data hasil pengukuran yang bersifat linier
intrinsik. Tetapi, kita terpaksa harus menelan rasa kecewa pada metode ini,
yakni ketika data yang kita peroleh tidak memiliki sifat linier. Mengapa ?
Karena penggunaan metode regresi linier seperti dipaksakan hanya untuk mengikuti
ambisi kita bahwa grafik hasil pengukuran harus linier. Nah, untuk mengobati
rasa kecewa tersebut pada pasal ini kita akan membahas regresi polinomial yang
mana untuk beberapa kasus metode ini akan memberikan hasil yang lebih cocok
dengan kenyataan.
Prinsip dari metode kuadrat terkecil dapat diperluas lagi
untuk pencocokan data hasil pengukuran kepada sebuah polinomial orde tertentu .
secara umum, polinomial berorde ke N dapat dituliskan sebagai
Simpangan kurva
terhadap tiap-tiap titik data dapat
dinyatakan sebagai
dimana M adalah
jumlah titik data. Selanjutnya, total kuadrat simpangannya dinyatakan oleh
Untuk memperoleh harga-harga koefisien polinomial, maka kita harus
menurunkan secara parsial persamaan 27) terhadap koefisien-koefisien
tersebut. Pada keadaan dimana total simpangannya berada pada titik ekstrim,
maka turunannya sama dengan nol.
Persamaan-persamaan pada 28) selanjutnya akan kita susun kembali untuk
memperoleh bentuk yang lebih manis, sehingga lebih mudah untuk ditangani.
Pernyataan 29) dapat kita nyatakan dalam bentuk matriks yaitu,
Harga koefisien-koefisien polinomial di atas dapat ditentukan dengan cara
menyelesaikan persamaan linier simultan 30) misalnya dengan metode eliminasi
Gauss atau Gauss-Jordan.
5. Pencocokan Data
kepada Kurva Kombinasi Linier Fungsi-Fungsi
Ide dasar dari pencocokan kurva dengan kombinasi linier
fungsi-fungsi ini sebenarnya berasal regresi polinomial. Lalu apa bedanya?
Bedanya adalah, jika pada regresi polinomial kita menggunakan kombinasi linier
fungsi dengan argumen sejenis dan orde yang berbeda atau kita biasa menyebutnya
dengan polinomial, sedangkan pencocokan kurva yang akan kita bahas ini
menggunakan kombinasi linier dari fungsi-fungsi yang tidak sejenis.
Secara umum, polinomial sebagai kombinasi dari
fungsi-fungsi tidak sejenis dapat dinyatakan sebagai
dengan y1, y2, y3, ... merupakan fungsi-fungsi yang telah diketahui,
dan a1, a2, a3, ... adalah
koefisien-koefisien yang akan ditentukan kemudian dan  adalah jumlah total fungsi yang kita
kombinasikan secara linier.
adalah jumlah total fungsi yang kita
kombinasikan secara linier.
Seperti halnya dengan beberapa metode yang telah dibahas
di depan, maka simpangan dari tiap-tiap titik data terhadap fungsi kurva yang
digunakan untuk pencocokan didefinisikan oleh
Total kuadrat simpangan 18) didefinisikan sebagai
Untuk memperoleh harga koefisien-koefisien a1, a2, a3, ... maka kita perlu melakukan pengambilan
derivatif parsial D terhadap
koefisien-koefisien tersebut dengan nol, sehingga kita bertemu lagi dengan
pernyataan
Jika persamaan 34) diperlihatkan secara eksplisit berbentuk
Penampilan dalam bentuk matriks pernyataan (2-35) menjadi lebih sederhana
yaitu,
Persamaan 36) memiliki N buah persamaan dengan N koefisien tak diketahui. Penyelesaian dari
persamaan linier simultan ini dapat dilakukan dengan menggunakan metode
eliminasi Gauss atau Gauss-Jordan (Rendi, 2014).
Persamaan Kurva Orde Tinggi
Dalam
menentukan persamaan kurva, kita bisa menggunakan salah satu contoh aplikasi
integral. Lebih lanjut ini digunakan pada berbagai ilmu terapan seperti
matematika, ekonomi dan lainnya. Misalkan dalam menentukan persamaan kurva
keseimbangan permintaan dan penawaran. Dari jejak garis, akan terlihat gradien
garis dan bisa dicari persamaan kurva yang dilaluinya.
Pembahasan di
sini kita batasi sekedar bagaimana menentukan persamaan kurva dari sebuah
fungsi/gradien garis yang diketahui dengan menggunakan integral. Sebagai
pengantar awal, kita harus ingat kembali pengertian dan defenisi integral.
Integral adalah bentuk anti-turunan dari sebuah fungsi, dimana
Berdasarkan definisi
integral dan turunan di atas, artinya jika diketahui turunan maka untuk mencari
F(x) cukup diintegralkan. Secara umum langkah menentukan persamaan kurva atau
grafik dengan integral sebagai berikut,
1. Integralkan Fungsi. Perlu diperhatikan apakah yang
diberikan turunan pertama, turunan kedua atau turunan ke berapa.
2.
Gunakan nilai yang diketahui di soal untuk menentukan
nilai konstanta C.
3.
Tulis persamaan kurva dengan sempurna.
3. Pencocokan Data
Menggunakan Fungsi Berpangkat
Fungsi
berpangkat merupakan fungsi matematis yang memiliki bentuk umum
dengan a dan b merupakan konstanta-konstanta persamaan linier yang akan ditentukan melalui teknik regresi linier. Untuk menerapkan metode kuadrat terkecil pada persamaan 18) tersebut, maka kita harus mengambil logaritma alamiahnya pada kedua ruas persamaan sehingga diperoleh ungkapan
Dengan
menggunakan definisi
maka persamaan
(2-19) dapat kita tuliskan kembali menjadi
v = bu + c ... 21)
yang merupakan
persamaan untuk garis lurus. Untuk menerapkan metode kuadrat terkecil pada
masalah ini, maka dapat dilakukan langkah-langkah analogi pada ungkapan 4)
sampai dengan 8) sehingga diperoleh ungkapan
Sehingga
harga-harga untuk konstanta a dan b dapat ditentukan melalui hubungan
Setelah ditemukan harga untuk parameter b dan c, maka harga a dapat ditemukan kembali melalui hubungan
4 Regresi
Polinomial
Pada pembahasan terdahulu kita telah membicarakan tentang
regresi linier yang bekerja pada data hasil pengukuran yang bersifat linier
intrinsik. Tetapi, kita terpaksa harus menelan rasa kecewa pada metode ini,
yakni ketika data yang kita peroleh tidak memiliki sifat linier. Mengapa ?
Karena penggunaan metode regresi linier seperti dipaksakan hanya untuk mengikuti
ambisi kita bahwa grafik hasil pengukuran harus linier. Nah, untuk mengobati
rasa kecewa tersebut pada pasal ini kita akan membahas regresi polinomial yang
mana untuk beberapa kasus metode ini akan memberikan hasil yang lebih cocok
dengan kenyataan.
Prinsip dari metode kuadrat terkecil dapat diperluas lagi
untuk pencocokan data hasil pengukuran kepada sebuah polinomial orde tertentu .
secara umum, polinomial berorde ke N dapat dituliskan sebagai
Simpangan kurva
terhadap tiap-tiap titik data dapat
dinyatakan sebagai
dimana M adalah
jumlah titik data. Selanjutnya, total kuadrat simpangannya dinyatakan oleh
Untuk memperoleh harga-harga koefisien polinomial, maka kita harus
menurunkan secara parsial persamaan 27) terhadap koefisien-koefisien
tersebut. Pada keadaan dimana total simpangannya berada pada titik ekstrim,
maka turunannya sama dengan nol.
Persamaan-persamaan pada 28) selanjutnya akan kita susun kembali untuk
memperoleh bentuk yang lebih manis, sehingga lebih mudah untuk ditangani.
Pernyataan 29) dapat kita nyatakan dalam bentuk matriks yaitu,
Harga koefisien-koefisien polinomial di atas dapat ditentukan dengan cara
menyelesaikan persamaan linier simultan 30) misalnya dengan metode eliminasi
Gauss atau Gauss-Jordan.
5. Pencocokan Data
kepada Kurva Kombinasi Linier Fungsi-Fungsi
Ide dasar dari pencocokan kurva dengan kombinasi linier
fungsi-fungsi ini sebenarnya berasal regresi polinomial. Lalu apa bedanya?
Bedanya adalah, jika pada regresi polinomial kita menggunakan kombinasi linier
fungsi dengan argumen sejenis dan orde yang berbeda atau kita biasa menyebutnya
dengan polinomial, sedangkan pencocokan kurva yang akan kita bahas ini
menggunakan kombinasi linier dari fungsi-fungsi yang tidak sejenis.
Secara umum, polinomial sebagai kombinasi dari
fungsi-fungsi tidak sejenis dapat dinyatakan sebagai
dengan y1, y2, y3, ... merupakan fungsi-fungsi yang telah diketahui,
dan a1, a2, a3, ... adalah
koefisien-koefisien yang akan ditentukan kemudian dan ![]() adalah jumlah total fungsi yang kita
kombinasikan secara linier.
adalah jumlah total fungsi yang kita
kombinasikan secara linier.
Seperti halnya dengan beberapa metode yang telah dibahas
di depan, maka simpangan dari tiap-tiap titik data terhadap fungsi kurva yang
digunakan untuk pencocokan didefinisikan oleh
Total kuadrat simpangan 18) didefinisikan sebagai
Untuk memperoleh harga koefisien-koefisien a1, a2, a3, ... maka kita perlu melakukan pengambilan
derivatif parsial D terhadap
koefisien-koefisien tersebut dengan nol, sehingga kita bertemu lagi dengan
pernyataan
Jika persamaan 34) diperlihatkan secara eksplisit berbentuk
Penampilan dalam bentuk matriks pernyataan (2-35) menjadi lebih sederhana
yaitu,
Persamaan 36) memiliki N buah persamaan dengan N koefisien tak diketahui. Penyelesaian dari
persamaan linier simultan ini dapat dilakukan dengan menggunakan metode
eliminasi Gauss atau Gauss-Jordan (Rendi, 2014).
Persamaan Kurva Orde Tinggi
Dalam
menentukan persamaan kurva, kita bisa menggunakan salah satu contoh aplikasi
integral. Lebih lanjut ini digunakan pada berbagai ilmu terapan seperti
matematika, ekonomi dan lainnya. Misalkan dalam menentukan persamaan kurva
keseimbangan permintaan dan penawaran. Dari jejak garis, akan terlihat gradien
garis dan bisa dicari persamaan kurva yang dilaluinya.
Pembahasan di
sini kita batasi sekedar bagaimana menentukan persamaan kurva dari sebuah
fungsi/gradien garis yang diketahui dengan menggunakan integral. Sebagai
pengantar awal, kita harus ingat kembali pengertian dan defenisi integral.
Integral adalah bentuk anti-turunan dari sebuah fungsi, dimana
Berdasarkan definisi
integral dan turunan di atas, artinya jika diketahui turunan maka untuk mencari
F(x) cukup diintegralkan. Secara umum langkah menentukan persamaan kurva atau
grafik dengan integral sebagai berikut,
1. Integralkan Fungsi. Perlu diperhatikan apakah yang
diberikan turunan pertama, turunan kedua atau turunan ke berapa.
2.
Gunakan nilai yang diketahui di soal untuk menentukan
nilai konstanta C.
3. Tulis persamaan kurva dengan sempurna.
Interpolasi dan Ekstrapolasi
Di dalam
pengertian matematika dasar, interpolasi adalah perkiraan suatu nilai tengah
dari satu set nilai yang diketahui. Interpolasi dalam arti luas merupakan upaya
mendefinisikan suatu fungsi dekatan suatu fungsi analitik yang tidak diketahui
atau pengganti fungsi rumit yang tak mungkin diperoleh persamaan analitiknya.
Nilai suatu fungsi y = f(x) diketahui berupa ordinat titik-titik x1,x2,x3,………,xn
yang diskontinu (discontinue) atau diskrit (discret). Ekspresi analitik y =
f( x) tidak diketahui. Ekstrapolasi yaitu suatu metode untuk memprediksikan
data diluar data-data yang diperoleh. Jadi metode ini digunakan untuk
memprediksikan data-data diluar data eksperimen yang kita dapatkan.
Terdapat
beberapa interpolasi dan ekstrapolasi, disini bergantung kepada persamaan
fungsi yang didapat, misal eksponensial, kuadrat, dan lain-lain.
Bab ini akan
membahas perkiraan ordinat atau f(x) secara numerik untuk nilai x yang berlaku di dalam interval (interpolasi)
maupun di luar interval titik-titik yang diketahui (ekstrapolasi). Permasalahan
utama dalam interpolasi dan ekstrapolasi adalah akurasi nilai yang
dihasilkannya. Fungsi interpolasi dan ekstrapolasi merupakan fungsi model
dengan bentuk tertentu yang bersifat umum supaya dapat mendekati fungsi-fungsi
yang dipakai secara luas. Sejauh ini fungsi yang umum digunakan adalah
polinomial dan trigonometri.
Proses
interpolasi dilaksanakan dalam dua tahap, yaitu pertama, menentukan fungsi
interpolasi yang merupakan kombinasi dari titik-titik (data) yang ada, dan
kedua, mengevaluasi fungsi interpolasi tersebut. Interpolasi dapat dilakukan
untuk kasus dengan dimensi lebih dari satu, misalnya fungsi f (x, y, z). Interpolasi multidimensi selalu
diselesaikan dengan urutan mulai dari interpolasi satu dimensi.
1.
Interpolasi Kedepan Cara Newton untuk Data dengan
Interval Konstan
Polinomial
interpolasi kedepan Newton F f(x) dengan x0 n-1 sebagai titik pusatnya yang mempunyai interval (Δx)
tetap sebesar h dapat dinyatakan sebagai berikut:
difference, sehingga interpolasi cara Newton yang
didasarkan pada persamaan 39) disebut dengan interpolasi kedepan cara Newton. Perbedaan kedepan
dihitung sebagai berikut:
Secara
skematis perbedaan kedepan diberikan dalam tabel berikut ini.
2. Ekstrapolasi
Kedepan Cara Newton untuk Data dengan Interval Konstan
Contoh :
Posisi planet
Mars diukur setiap 10 hari seperti ditunjukkan pada tabel. Dari data ini
diminta untuk memperkirakan posisi panet Mars pada t = 1450,5.
Jawaban:
Persoalan ini
merupakan masalah ekstrapolasi, karena harga yang diinginkan berada di luar
interval data-data yang diketahui. Ekstrapolasi dilakukan berdasar 5 data
terakhir, yaitu mulai t = 1300,5. Perhitungan perbedaan nilai kedepan diberikan
dalam tabel berikut ini.
Berikut dilampirkan powerpoint yang berkaitan dengan materi yang dibahas di blog ini yaitu mengenai pencocokan kurva
Terdapat
beberapa interpolasi dan ekstrapolasi, disini bergantung kepada persamaan
fungsi yang didapat, misal eksponensial, kuadrat, dan lain-lain.
Bab ini akan
membahas perkiraan ordinat atau f(x) secara numerik untuk nilai x yang berlaku di dalam interval (interpolasi)
maupun di luar interval titik-titik yang diketahui (ekstrapolasi). Permasalahan
utama dalam interpolasi dan ekstrapolasi adalah akurasi nilai yang
dihasilkannya. Fungsi interpolasi dan ekstrapolasi merupakan fungsi model
dengan bentuk tertentu yang bersifat umum supaya dapat mendekati fungsi-fungsi
yang dipakai secara luas. Sejauh ini fungsi yang umum digunakan adalah
polinomial dan trigonometri.
Proses
interpolasi dilaksanakan dalam dua tahap, yaitu pertama, menentukan fungsi
interpolasi yang merupakan kombinasi dari titik-titik (data) yang ada, dan
kedua, mengevaluasi fungsi interpolasi tersebut. Interpolasi dapat dilakukan
untuk kasus dengan dimensi lebih dari satu, misalnya fungsi f (x, y, z). Interpolasi multidimensi selalu
diselesaikan dengan urutan mulai dari interpolasi satu dimensi.
1.
Interpolasi Kedepan Cara Newton untuk Data dengan
Interval Konstan
Polinomial
interpolasi kedepan Newton F f(x) dengan x0 n-1 sebagai titik pusatnya yang mempunyai interval (Δx)
tetap sebesar h dapat dinyatakan sebagai berikut:
difference, sehingga interpolasi cara Newton yang
didasarkan pada persamaan 39) disebut dengan interpolasi kedepan cara Newton. Perbedaan kedepan
dihitung sebagai berikut:
2. Ekstrapolasi
Kedepan Cara Newton untuk Data dengan Interval Konstan
Contoh :
Posisi planet
Mars diukur setiap 10 hari seperti ditunjukkan pada tabel. Dari data ini
diminta untuk memperkirakan posisi panet Mars pada t = 1450,5.
Jawaban:
Persoalan ini
merupakan masalah ekstrapolasi, karena harga yang diinginkan berada di luar
interval data-data yang diketahui. Ekstrapolasi dilakukan berdasar 5 data
terakhir, yaitu mulai t = 1300,5. Perhitungan perbedaan nilai kedepan diberikan
dalam tabel berikut ini.
Berikut dilampirkan powerpoint yang berkaitan dengan materi yang dibahas di blog ini yaitu mengenai pencocokan kurva









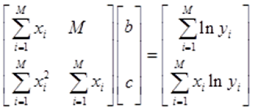


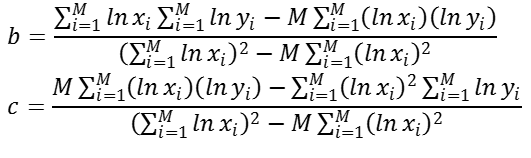














Tidak ada komentar:
Posting Komentar